Auswertung

Berücksichtigung von Drittvariablen

Bei der Datenauswertung können neben unabhängigen und abhängigen Variablen auch Drittvariablen Berücksichtigung finden. In der E-Learning Forschung sind Lernereigenschaften (z.B. Expertise) und die mit den Versuchsmaterialien verbrachte Zeit typische Beispiele für Drittvariablen. Diese Variablen können dabei in unterschiedlicher Form in die Analyse einfließen. Nachfolgend werden ausgewählte Möglichkeiten der Berücksichtigung von Drittvariablen vorgestellt:

• Kovarianzanalyse
• Median-Split
• Extremgruppenvergleich
• Regressionsanalysen
• Neuronale Netze

Neben diesen statistischen Verfahren kann auch auf Mediationsanalysen (Baron und Kenny, 1986) zurückgegriffen werden, die in der E-Learning Forschung neuerdings zum Einsatz kommen (z.B. Cierniak et al., 2009).

Kovarianzanalyse

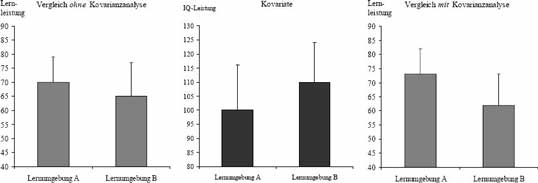
Die Kovarianzanalyse stellt eine besonders einfache Möglichkeit bereit, eine Drittvariable in die Datenanalyse einzubeziehen. Bei diesem statistischen Verfahren wird der Einfluss einer Drittvariablen – hier als Kovariate bezeichnet – auf die abhängigen Variablen rechnerisch konstant gehalten, d.h. ihr Einfluss wird herausgerechnet (herauspartialisiert). Sollen beispielsweise zwei elektronische Lernumgebungen hinsichtlich ihrer Lernwirksamkeit verglichen werden, so könnte die erfasste Intelligenz der Probanden als Kovariate fungieren. Nach Durchführung der Kovarianzanalyse besitzen zufällig entstandene Mittelswertunterschiede der IQ Leistungen keinen Einfluss mehr auf mögliche Lernleistungsunterschiede (abhängige Variable) zwischen den beiden Lernumgebungen.

Angenommen, die durchschnittliche Intelligenz der Probanden, welche die Lernumgebung A erhalten, läge zufallsbedingt bei 100, der IQ der Teilnehmer unter Lernumgebung B hingegen bei 110 (Abbildung 27 Mitte). Die Kovarianzanalyse erhöht nun rechnerisch den IQ-Mittelwert unter Bedingung A auf ungefähr 105. Der Mittelwert unter Bedingung B wird hingegen rechnerisch auf etwa 105 gesenkt. Wenn die Lernleistungen mit den Intelligenzleistungen korrelieren, führt die Veränderung der IQ-Werte unmittelbar zu Änderungen der Lernleistungen der beiden Bedingungen. In diesem fiktiven Fall würden durch die positive Korrelation zwischen IQ und Lernleistung die ohnehin schon höheren Lernleistungen unter Lernumgebung A noch weiter erhöht, während die Leistungen unter Bedingung B hingegen gesenkt werden (Abbildung 27).

Folgende Voraussetzungen müssen vorliegen, damit die Kovarianzanalyse einen (praktisch bedeutsamen) Einfluss bei der Datenanalyse annimmt (vgl. Bortz, 2005):

• Die Kovariate muss unterschiedliche Mittelwerte für die einzelnen Bedingungskombinationen annehmen. Liegen die IQ-Leistungen für Lernumgebung A und B zum Beispiel beide bereits exakt bei 105, dann führt die Kovarianzanalyse zu keiner Veränderung der Lernleistungen.
• Die Kovariate muss mit der abhängigen Variable korrelieren. Hängen beispielsweise Intelligenz- und Lernleistungen nicht miteinander zusammen, d.h. liegt die Korrelation exakt bei Null, dann führt die Kovarianzanalyse zu keiner Veränderung der Lernleistungen.

Sind die genannten Voraussetzungen erfüllt, kann die Kovarianzanalyse zu zwei unterschiedlichen Ergebnissen führen:

• Unterschiede zwischen verschiedenen Versuchsbedingungen verstärken sich (wie in Abbildung 27 illustriert). Durch die Durchführung der Kovarianzanalyse können zuvor nicht signifikante Ergebnisse statistisch bedeutsam werden.
• Unterschiede zwischen verschiedenen Versuchsbedingungen verringern sich. Dies kann soweit führen, dass signifikante Differenzen durch Berücksichtigung von Kovariaten nicht mehr überzufällig bedeutsam sind. In diesem Fall könnte man vermuten, dass Leistungsdifferenzen zwischen verschiedenen Versuchsgruppen nur durch unterschiedliche Ausprägungen der Kovariate bedingt gewesen sind.

Die Kovarianzanalyse ist eine einfache Methode, Drittvariablen bei der Datenauswertung zu berücksichtigen. Der potentiell störende Effekt durch die Drittvariable wird rechnerisch neutralisiert und somit ein möglicher Einfluss vermieden (vgl. hier). Komplexe Zusammenhänge, die durch die Drittvariable bedingt sind, werden durch die Kovarianzanalyse jedoch nicht aufgedeckt.